毎年、厚生労働省から公開されている簡易生命表(詳細は、厚生統計協会より発行されている簡易生命表を参照)の情報を用います。
簡易生命表では、99歳までの死亡率のみ公表されているため、100歳から114歳までの1年間の死亡率を、Gompertz-Makeham係数を用いて外挿(推測)します。
外挿(推測)式は、以下の通りです。
1年生存確率=exp{-(A+B/C*(EXP(C)-1)*EXP(C*(age-Cx))}
上記式におけるGompertz-Makeham係数(A値、B値、C値)とこの係数をあてはめ始める年齢(Cx値)は、毎年簡易生命表において公表されています。詳細は、平成12年簡易生命表(厚生労働省大臣官房統計情報部編:財団法人 厚生統計協会発行)の「II 平成12年簡易生命表の作成方法」をご参照下さい。
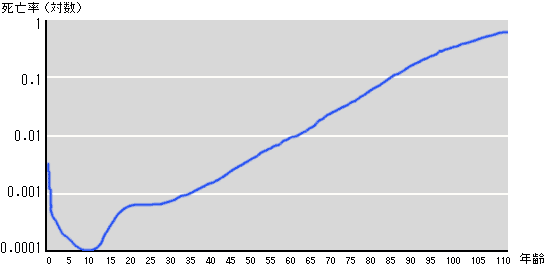
(男性、86歳以降のみ:平成12年簡易生命表をもちいた計算)
(文献)
有本弘子、北川千恵子、荒井 博:Cohort 生存率表について.厚生の指標 32:25-30,1985
(この論文中の式(5)に誤植があります。正確には、上記式もしくは、簡易生命表で出版されている式を参照ください)
■附記
1962年から1980年(昭和55年)までは、簡易生命表から小池らの方法を用いて、114歳までの生存確率(もしくは"1−死亡率")を計算していました。
以下小池らの文献より抜粋.
算出方法
x歳時の死亡率をqとすると、このqは、高年齢では、近似的に成長曲線になることを利用して、
log[(1-q)/q]≒ax+b とおき
S1=Σlog[(1-q)/q]≒aΣx+12b (x=61歳から72歳まで)・・・・・・・・・1)
S2=Σlog[(1-q)/q]≒aΣx+12b (x=73歳から84歳まで)・・・・・・・・・2)
を解いて、aとbをもとめ、
log[(1-q)/q]≒ax+b を変形し、
q = 1/(log-1(ax+b)+1) とし、
これにx=85〜99(今回のコホート生存率表では、114歳まで)歳を代入して、qを計算し、1−qをx歳の生存率とした。
(文献)
小池淳夫、田代節春「コホート生存率表」厚生の指標、第23巻(第3号)p14-27, 昭和51年
